Advertisements
Advertisements
Question
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Solution
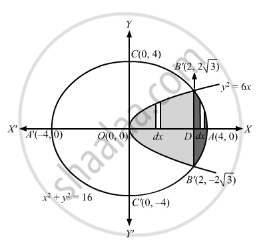
Points of intersection of the parabola and the circle is obtained by solving the simultaneous equations
\[x^2 + y^2 = 16\text{ and }y^2 = 6x\]
\[ \Rightarrow x^2 + 6x = 16 \]
\[ \Rightarrow x^2 + 6x - 16 = 0\]
\[ \Rightarrow \left( x + 8 \right)\left( x - 2 \right) = 0\]
\[ \Rightarrow x = 2\text{ or }x = - 8 ,\text{ which is not the possible solution . }\]
\[ \therefore\text{ When }x = 2, y = \pm \sqrt{6 \times 2} = \pm \sqrt{12} = \pm 2\sqrt{3}\]
\[ \therefore B\left( 2 , 2\sqrt{3} \right)\text{ and B'}\left( 2 , - 2\sqrt{3} \right)\text{ are points of intersection of the parabola and circle . }\]
\[\text{ Now, Required area = area }\left(\text{ OBAB'O }\right) \]
\[ = 2\text{ area }\left(\text{ OBAO }\right)\]
\[ = 2\left\{ \text{ area }\left(\text{ OBDO }\right) +\text{ area }\left( \text{ DBAD }\right) \right\}\]
\[ = 2 \times \left[ \int_0^2 \sqrt{6x}dx + \int_2^4 \sqrt{16 - x^2} dx \right]\]
\[ = 2 \times \left\{ \left[ \sqrt{6}\frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^2 + \left[ \frac{1}{2}x\sqrt{16 - x^2} + \frac{1}{2} \times 16 \sin^{- 1} \left( \frac{x}{4} \right) \right]_2^4 \right\}\]
\[ = 2 \times \left\{ \left( \sqrt{6} \times \frac{2}{3} \times 2^\frac{3}{2} - 0 \right) + \left( \frac{1}{2}4\sqrt{16 - \left( 4 \right)^2} + \frac{1}{2} \times 16 \sin^{- 1} \frac{4}{4} - \frac{1}{2} \times 2\sqrt{16 - 2^2} - \frac{1}{2} \times 16 \sin^{- 1} \frac{2}{4} \right) \right\}\]
\[ = 2 \times \left\{ \left( \sqrt{6} \times \frac{2}{3} \times 2\sqrt{2} \right) + 0 + 8 \sin^{- 1} \left( 1 \right) - \sqrt{12} - 8 \sin^{- 1} \left( \frac{1}{2} \right) \right\}\]
\[ = 2 \times \left[ \frac{8\sqrt{3}}{3} + 8 \times \frac{\pi}{2} - 2\sqrt{3} - 8\frac{\pi}{6} \right]\]
\[ = 2 \left\{ \frac{8\sqrt{3} - 6\sqrt{3}}{3} + 8\left( \frac{\pi}{2} - \frac{\pi}{6} \right) \right\}\]
\[ = 2\left\{ \frac{2\sqrt{3}}{3} + 8\left( \frac{2\pi}{6} \right) \right\}\]
\[ = \frac{4\sqrt{3}}{3} + \frac{16\pi}{3}\]
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3, is
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
