Advertisements
Advertisements
Question
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
Solution
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to `297/6`sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.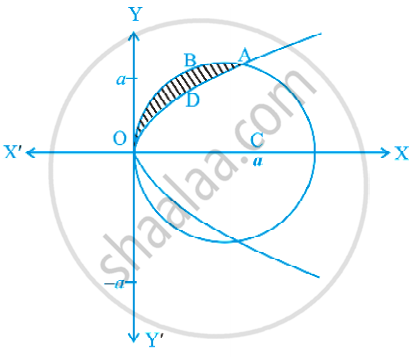
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
