Advertisements
Advertisements
Question
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
Solution
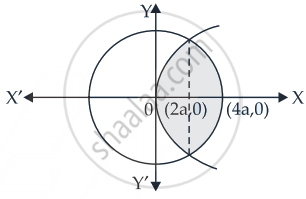
Given that: {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}
Equation of Parabola is y2 = 6ax .....(i)
And equation of circle is x2 + y2 ≤ 16a2 .....(ii)
Solving equation (i) and (ii)
We get x2 + 6ax = 16a2
⇒ x2 + 6ax – 16a2 = 0
⇒ x2 + 8ax – 2ax – 16a2 = 0
⇒ x(x + 8a) – 2a(x + 8a) = 0
⇒ (x + 8a)(x – 2a) = 0
∴ x = 2a and x = – 8a. .....(Rejected as it is out of region)
Area of the required shaded region
= `2[int_0^(2"a") sqrt(6"a"x) "d"x + int_(2"a")^(4"a") sqrt(16"a"^2 - x^2) "d"x]`
= `2[sqrt(6"a") int_0^(2"a") sqrt(x) "d"x + int_(2"a")^(4"a") sqrt((4"a")^2 - x^2) "d"x]`
= `2sqrt(6"a") * 2/3 * [x^(3/2)]_0^(2"a") + 2[x/2 sqrt((4"a")^2 - x^2) + (16"a"^2)/2 sin^-1 x/(4"a")]_(2"a")^(4"a")`
= `(4sqrt(6))/3 * sqrt("a") [(2"a")^(3/2) - 0] + [xsqrt((4"a")^2 - x^2) + 16"a"^2 sin^-1 x/(4"a")]_(2"a")^(4"a")`
= `(8sqrt(12))/3 "a"^2 + [16"a"^2 8sin^-1 (1) - 2"a"sqrt(12"a"^2) - 16"a"^2 sin^-1 1/2]`
= `(16sqrt(13))/3 "a"^2 + [16"a"^2 * pi/2 - 2"a" * 2sqrt(3)"a" - 16"a"^2 * pi/6]`
= `(16sqrt(3))/3 "a"^2 + 8pi"a"^2 - 4sqrt(3)"a"^2 - 8/3 pi"a"^2`
= `((16sqrt(3))/3 - 4sqrt(3))"a"^2 + 16/3 pi"a"^2`
= `(4sqrt(3))/3 "a"^2 + 16/3 pi"a"^2`
= `4/3 (sqrt(3) + 4pi)"a"^2`
Hence, required area = `4/3(sqrt(3) + 4pi)"a"^2` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
