Advertisements
Advertisements
Question
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Solution
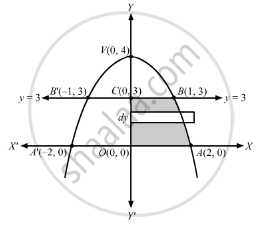
\[y = 4 - x^2\text{ is a parabola, with vertex (0, 4), opening downwars and having axis of symmetry as - ve }y -\text{ axis }\]
\[y = 0\text{ is the }x - \text{ axis, cutting the parabola at }A(2, 0)\text{ and A'}( - 2, 0)\]
\[y = 3\text{ is a line parallel to }x - \text{ axis, cutting the parabola at B }(1, 3 )\text{ and B'}( - 1, 3) \text{ and }y -\text{ axis at }C(0, 3) \]
\[\text{ Required area is the shaded area ABB'A }= 2 \left(\text{ area ABCO }\right)\]
\[\text{ Consider a horizontal strip of length }= \left| x_2 - x_1 \right|\text{ and width = dy in the shaded region }\]
\[\text{ Area of approximating rectangle }= \left| x_2 - x_1 \right| dy\]
\[\text{ The approximating rectangle moves from }y = 0\text{ to }y = 3 \]
\[ \therefore\text{ Area of shaded region }= 2 \int_3^0 \left| x_2 - x_1 \right| dy \]
\[ \Rightarrow A = 2 \int_0^3 \left( x_2 - x_1 \right) dy ...............\left[ As, \left| x_2 - x_1 \right| = x_2 - x_{1 ,} x_2 > x_1 \right] \]
\[ \Rightarrow A = 2 \int_0^3 \left( \sqrt{4 - y} - 0 \right) dy\]
\[ \Rightarrow A = - 2 \left[ \frac{\left( 4 - y \right)^\frac{3}{2}}{\frac{3}{2}} \right]_0^3 \]
\[ \Rightarrow A = - 2 \left[ \frac{\left( 4 - y \right)^\frac{3}{2}}{\frac{3}{2}} \right]_0^3 \]
\[ \Rightarrow A = 2 \times \frac{2}{3}\left[ 4^\frac{3}{2} - 1^\frac{3}{2} \right]\]
\[ \Rightarrow A = \frac{4}{3} \times 7 \]
\[ \Rightarrow A = \frac{28}{3}\text{ sq . units }\]
\[ \therefore \text{ Area bounded by the two parabolas }= \frac{28}{3}\text{ sq . units }\]
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Find the area of the region bounded by the curve y = sinx, the lines x=-π/2 , x=π/2 and X-axis
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Find the area common to the circle x2 + y2 = 16 a2 and the parabola y2 = 6 ax.
OR
Find the area of the region {(x, y) : y2 ≤ 6ax} and {(x, y) : x2 + y2 ≤ 16a2}.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region included between y2 = 9x and y = x
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤ `pi/2` is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
