Advertisements
Advertisements
Question
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
Solution
The area of the region bounded by the curve, y2 = x, the line x = `1/4` and x = 4 and y = 0 (i.e., x-axis) is the a ABEF
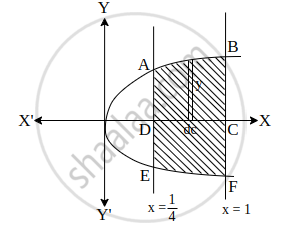
Thus, area of ABEF = 2 area of ABCD
= `2int_(1/4)^1 ydx`
= `2int_(1/4)^1 sqrt(x)dx`
= `2[x^(3/2)/(3/2)]_(1/4)^1`
= `4/3[(1)^(3/2) - (1/4)^(3/2)]`
= `4/3[1 - 1/8]`
= `4/3[7/8]`
= `7/6` units
APPEARS IN
RELATED QUESTIONS
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
The area bounded by the curve y = x | x|, x-axis and the ordinates x = –1 and x = 1 is given by ______.
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Make a rough sketch of the graph of the function y = 4 − x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x-axis and the lines x = 0 and x = 2.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region bounded by y = | x − 1 | and y = 1.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.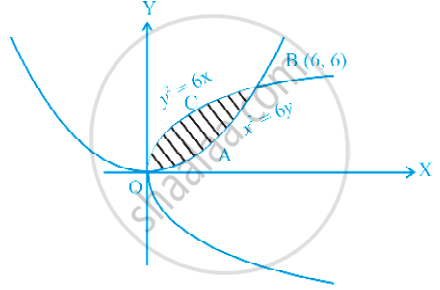
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.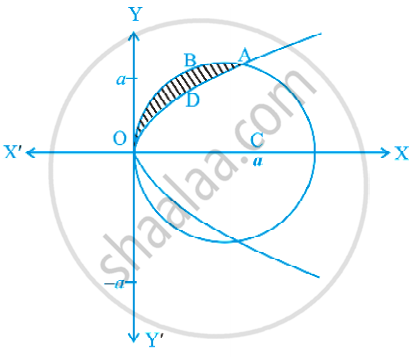
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
The area bounded by `y`-axis, `y = cosx` and `y = sinx, 0 ≤ x - (<pi)/2` is
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
