Advertisements
Advertisements
Question
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
Solution
y2 = 4x is a right-handed parabola with vertex at O(0,0) and axis of parabola is x- axis.
y = x is a line passing through origin O(0,0)
Now, Finding their intersection
y2 = 4x
⇒ x2 = 4x
⇒ x2 - 4x = 0
⇒ x(x - 4) = 0
⇒ x = 0 and x = 4
Also y = x ⇒ y = 0 and y = 4
∴ Points of intersections are (0,0) and (4,4)
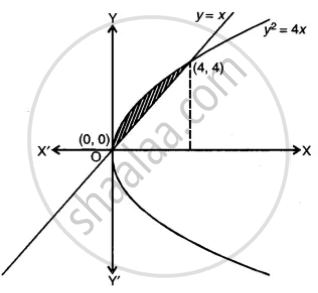
Required area = `2 int_0^4 sqrt"x" "dx" - int_0^4 "x" "dx"`
`= 2["x"^(3/2)/(3/2)]_0^4 - ["x"^2/2]_0^4`
`= 2xx2/3 |(4)^(3/2) - 0| - |4^2/2 -0 |`
`= 4/3 xx 8 - 8`
`= (32 - 24)/3 = 8/3`
`= 2 8/3 "sq.units"`
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Find the area bounded by the curve y = cos x, x-axis and the ordinates x = 0 and x = 2π.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Evaluate:
`int_0^1x^2dx`
