Advertisements
Advertisements
Question
Sketch the region bounded by the curves
Solution
Consider the given equation
This equation represents a semicircle with centre at
the origin and radius = sqrt5 units
Given that the region is bounded by the above
semicircle and the line y = |x-1|
Let us find the point of intersection of the
given curve meets the line y= |x - 1|
Squaring both the sides, we have,
When x = -1,y = 2
When x = 2,y = 1
Consider the following figure.
Thus the intersection points are ( -1,2) and (2,1)
Consider the following sketch of the bounded region.
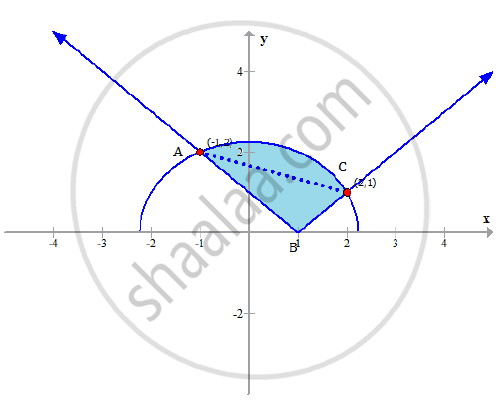
Required Area, A=
=
Required area=
APPEARS IN
RELATED QUESTIONS
Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Draw a rough sketch of the curve
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
If the area bounded by the parabola
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.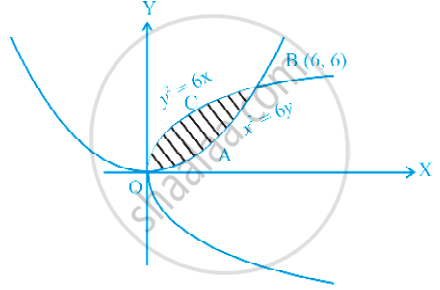
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is
The area bounded by the curve
Let the curve y = y(x) be the solution of the differential equation,
Evaluate:
