Advertisements
Advertisements
प्रश्न
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
उत्तर
y = 6x - x2, y = x2 - 2x
x2 - 6x = - y
⇒ x2 - 6x + 9 = - y + 9
⇒ ( x - 3 )2 = - ( y - 9 )
This represents a downward parabola with vertex (3, 9) ...(i)
y = x2 - 2x
x2 - 2x + 1 = y + 1
⇒ ( x - 1 )2 = y + 1
⇒ ( x -1 )2 = y - ( -1 ) ...(ii)
This represents an upward parabola with vertex (1, -1)
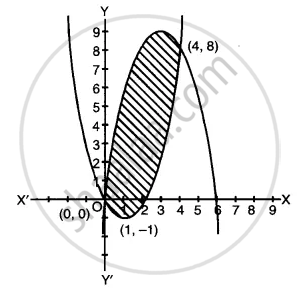
Point of intersection is given by:
6x - x2 = x2 - 2x
⇒ 2x2 = 8x
⇒ x2 - 4x = 0
⇒ x (x - 4) = 0
x = 0, x = 4
y = 6 x 4 - 42
= 24 - 16 = 8
Point of intersection is (0, 0) ; (4, 8)
Reqd. area = ` int_0^4 (6x - x^2) - (x^2 - 2x) dx`
= `int_0^4 8x - 2x^2 dx = [ (8x^2)/(2) - (2)/(3) x^3]_0^4`
= 4 x 42 - `(2)/(3) (4)^3 = (64)/(3)` sq. units.
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area bounded by the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and the ordinates x = ae and x = 0, where b2 = a2 (1 − e2) and e < 1.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Find the area of the region bounded by y = | x − 1 | and y = 1.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
