Advertisements
Advertisements
प्रश्न
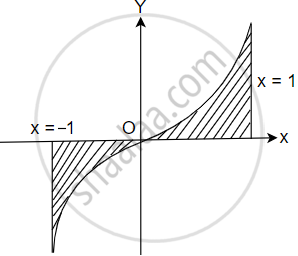
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
उत्तर
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
The area bounded by the curve y = x | x|, x-axis and the ordinates x = –1 and x = 1 is given by ______.
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2.
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤ `pi/2` is ______.
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
Using integration, find the area of the region bounded by line y = `sqrt(3)x`, the curve y = `sqrt(4 - x^2)` and Y-axis in first quadrant.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
