Advertisements
Advertisements
प्रश्न
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
उत्तर
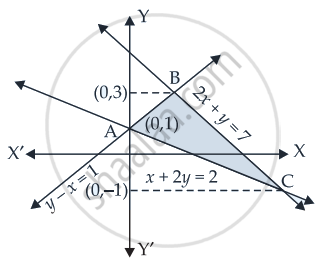
Given that: x + 2y = 2 .....(i)
y – x = 1 ......(ii)
And 2x + y = 7 ......(iii)
| x | 0 | 2 |
| y | 1 | 0 |
| x | 0 | –1 |
| y | 1 | 0 |
| x | 0 | `7/2` |
| y | 7 | 0 |
Solving equations (ii) and (iii)
We get y = 1 + x
∴ 2x + 1 + x = 7
3x = 6
⇒ x = 2
∴ y = 1 + 2
= 3
Coordinates of B = (2, 3)
Solving equations (i) and (iii)
We get x + 2y = 2
∴ x = 2 – 2y
2x + y = 7
2(2 – 2y) + y = 7
⇒ 4 – 4y + y = 7
⇒ –3y = 3
∴ y = –1 and x = 4
∴ Coordinates of C = (4, – 1) and coordinates of A = (0, 1).
Taking the limits on y-axis, we get
`int_(-1)^3 x_"BC" "d"y - int_(-1)^1 x_"AC" "d"y - int_1^3 x_"AB" "d"y`
= `int_(-1)^3 (7 - y)/2 "d"y - int_(-1)^1 (2 - 2y) "d"y - int_1^3 (y - 1) "d"y`
= `1/2 [7y - y^2/2]_-1^2 - 2[y - y^2/2]_-1^1 - [y^2/2 - y]_1^3`
= `1/2[(21 - 9/2) - (7 - 1/2)] - 2[(1 - 1/2) - (-1 - 1/2)] - [(9/2 - 3) - (1/2 - 1)]`
= `1/2[33/2 + 15/2] - 2[1/2 + 3/2] - [3/2 + 1/2]`
= `1/2 xx 24 - 2 xx 2 - 2`
⇒ 12 – 4 – 2 = 6 sq.units
Hence, the required area = 6 sq.units
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Draw a rough sketch of the curve and find the area of the region bounded by curve y2 = 8x and the line x =2.
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area bounded by the curve y = cos x, x-axis and the ordinates x = 0 and x = 2π.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Using integration find the area of the region bounded by the curves \[y = \sqrt{4 - x^2}, x^2 + y^2 - 4x = 0\] and the x-axis.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area of the region formed by x2 + y2 − 6x − 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is ______ .
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
