HSC Science (General)
HSC Arts (English Medium)
HSC Science (Electronics)
HSC Science (Computer Science)
Academic Year: 2013-2014
Date: March 2014
Advertisements
Which of the following represents direction cosines of the line :
(a)`0,1/sqrt2,1/2`
(b)`0,-sqrt3/2,1/sqrt2`
(c)`0,sqrt3/2,1/2`
(d)`1/2,1/2,1/2`
Chapter: [0.08] Three Dimensional Geometry
`A=[[1,2],[3,4]]` ans A(Adj A)=KI, then the value of 'K' is
2
- 2
10
-10
Chapter: [0.02] Matrices
The general solution of the trigonometric equation tan2 θ = 1 is ____________
`theta =npi+-(pi/3),n in z`
`theta =npi+-pi/6, n in z`
`theta=npi+-pi/4, n in z`
`0=npi, n in z`
Chapter: [0.03] Trigonometric Functions
If `bara, barb, bar c` are the position vectors of the points A, B, C respectively and ` 2bara + 3barb - 5barc = 0` , then find the ratio in which the point C divides line segment AB.
Chapter: [0.07] Vectors
The Cartestation equation of line is `(x-6)/2=(y+4)/7=(z-5)/3` find its vector equation.
Chapter: [0.013999999999999999] Pair of Straight Lines [0.09] Line
Equation of a plane is `vecr (3hati-4hatj+12hatk)=8`. Find the length of the perpendicular from the origin to the plane.
Chapter: [0.1] Plane
Find the acute angle between the lines whose direction ratios are 5, 12, -13 and 3, - 4, 5.
Chapter: [0.08] Three Dimensional Geometry
Write the dual of the following statements: (p ∨ q) ∧ T
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
Write the dual of the following statements:
Madhuri has curly hair and brown eyes.
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
If the lines `(x-1)/2=(y+1)/3=(z-1)/4 ` and `(x-3)/1=(y-k)/2=z/1` intersect each other then find value of k
Chapter: [0.016] Line and Plane [0.09] Line
Prove that three vectors `bara, barb and barc ` are coplanar, if and only if, there exists a non-zero linear combination `xbara + ybarb + z barc = bar0`.
Chapter: [0.07] Vectors
Using truth table prove that ∼p ˄ q ≡ (p ˅ q) ˄ ∼p
Chapter: [0.01] Mathematical Logic [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
In any ΔABC, with usual notations, prove that b2 = c2 + a2 – 2ca cos B.
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
Show that the equation `x^2-6xy+5y^2+10x-14y+9=0 ` represents a pair of lines. Find the acute angle between them. Also find the point of intersection of the lines.
Chapter: [0.04] Pair of Straight Lines
Advertisements
Express the following equations in the matrix form and solve them by method of reduction :
2x- y + z = 1, x + 2y + 3z = 8, 3x + y - 4z =1
Chapter: [0.02] Matrices
Show that every homogeneous equation of degree two in x and y, i.e., ax2 + 2hxy + by2 = 0 represents a pair of lines passing through origin if h2−ab≥0.
Chapter: [0.04] Pair of Straight Lines
Find the symbolic form of the following switching circuit, construct its switching table and interpret it.
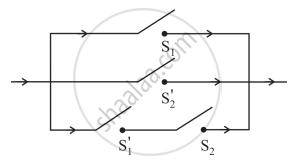
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
If A, B, C, D are (1, 1, 1), (2, 1, 3), (3, 2, 2), (3, 3, 4) respectively, then find the volume of parallelopiped with AB, AC and AD as the concurrent edges.
Chapter: [0.015] Vectors [0.07] Vectors
Find the equation of the plane passing through the line of intersection of planes 2x – y + z = 3 and 4x – 3y + 5z + 9 = 0 and parallel to the line `(x + 1)/2 = (y + 3)/4 = (z - 3)/5`
Chapter: [0.1] Plane
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
Chapter: [0.017] Linear Programming [0.11] Linear Programming Problems
Show that:
`cos^(-1)(4/5)+cos^(-1)(12/13)=cos^(-1)(33/65)`
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
If y =1 - cos θ , x = 1 - sin θ , then ` dy/dx at " "θ =pi/4` is ________
Chapter: [0.13] Differentiation
The integrating factor of linear differential equation `dy/dx+ysecx=tanx` is
(a)secx- tan x
(b) sec x · tan x
(c)sex+tanx
(d) secx.cotx
Chapter: [0.17] Differential Equation
The equation of tangent to the curve y = 3x2 - x + 1 at the point (1, 3) is
(a) y=5x+2
(b)y=5x-2
(c)y=1/5x+2
(d)y=1/5x-2
Chapter: [0.06] Conics
Examine the continuity of the function
f(x) =sin x- cos x, for x ≠ 0
=- 1 ,forx=0
at the poinl x = 0
Chapter: [0.12] Continuity
Verify Rolle's theorem for the function
f(x)=x2-5x+9 on [1,4]
Chapter: [0.14] Applications of Derivative
Evaluate : `intsec^nxtanxdx`
Chapter: [0.15] Integration
Advertisements
The probability mass function (p.m.f.) of X is given below:
| X=x | 1 | 2 | 3 |
| P (X= x) | 1/5 | 2/5 | 2/5 |
find E(X2)
Chapter: [0.19] Probability Distribution
Given that X~ B(n = 10, p), if E(X) = 8. find the value of p.
Chapter: [0.18] Statistics
Ify y=f(u) is a differentiable function of u and u = g(x) is a differentiable function of x then prove that y = f (g(x)) is a differentiable function of x and
`(dy)/(dx)=(dy)/(du)*(du)/(dx)`
Chapter: [0.13] Differentiation
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y = A cos (log x) + B sin (log x)
Chapter: [0.026000000000000002] Differential Equations
Evaluate : `int x^2/((x^2+2)(2x^2+1))dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
An open box is to be made out of a piece of a square card board of sides 18 cms by cutting off equal squares from the comers and turning up the sides. Find the maximum volume of the box.
Chapter: [0.022000000000000002] Applications of Derivatives [0.14] Applications of Derivative
Prove that:
`int_0^(2a)f(x)dx = int_0^af(x)dx + int_0^af(2a - x)dx`
Chapter: [0.026000000000000002] Differential Equations [0.17] Differential Equation
If the function f (x) is continuous in the interval [-2, 2],find the values of a and b where
`f(x)=(sinax)/x-2, for-2<=x<=0`
`=2x+1, for 0<=x<=1`
`=2bsqrt(x^2+3)-1, for 1<x<=2`
Chapter: [0.12] Continuity
Solve the differential equation `dy/dx=(y+sqrt(x^2+y^2))/x`
Chapter: [0.17] Differential Equation
A fair coin is tossed 8 times. Find the probability that it shows heads at least once
Chapter: [0.027999999999999997] Binomial Distribution [0.2] Bernoulli Trials and Binomial Distribution
If xpyq = (x + y)p+q then Prove that `dy/dx = y/x`
Chapter: [0.021] Differentiation [0.13] Differentiation
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Chapter: [0.16] Applications of Definite Integral
Prove that:
`int sqrt(x^2 - a^2)dx = x/2sqrt(x^2 - a^2) - a^2/2log|x + sqrt(x^2 - a^2)| + c`
Chapter: [0.023] Indefinite Integration [0.15] Integration
A random variable X has the following probability distribution :
| X=x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P[X=x] | k | 3k | 5k | 7k | 9k | 11k | 13k |
(a) Find k
(b) find P(O <X< 4)
(c) Obtain cumulative distribution function (c. d. f.) of X.
Chapter: [0.19] Probability Distribution
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 12th Standard Board Exam Mathematics and Statistics with solutions 2013 - 2014
Previous year Question paper for Maharashtra State Board 12th Standard Board Exam Maths and Stats-2014 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics and Statistics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 12th Standard Board Exam.
How Maharashtra State Board 12th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Mathematics and Statistics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
