Advertisements
Advertisements
Question
Find the equation of the normal at a point on the curve x2 = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.
Solution
Equations of the given circles are
`x^2+y^2=4 ................(1)`
`(x-2)^2+y^2=4...........(2)`
Equation (1) is a circle with centre O at the origin and radius 2. Equation (2) is a circle with centre C (2, 0) and radius 2. Solving equations (1) and (2), we have
`(x-2)^2+y^2=x^2+y^2`
`or x^2-4x+4+y^2=x^2+y^2`
or x=1 which gives `y=+-sqrt3`
Thus, the points of intersection of the given circles are `A(1,sqrt3) and A'(1,-sqrt3) ` as shown in the Figure
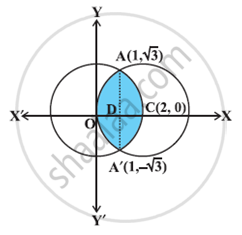
Required area of the enclosed region OACA′O between circles
= 2 [area of the region ODCAO]
= 2 [area of the region ODAO + area of the region DCAD]
`=2[int_0^1ydx+int_1^2ydx]`
`=2[int_0^1sqrt(4-(x-2)^2)dx+int_1^2sqrt(4-x^2)dx]`
`=2[1/2(x-2)sqrt(4-(x-2)^2)+1/2xx4sin^(-1)((x-2)/2)]_0^1+2[1/2xsqrt(4-x^2)+1/2xx4sin^(-1)(x/2)]_1^2`
`=[(x-2)sqrt(4-(x-2)^2)+4sin^(-1)((x-2)2)]_0^1+[xsqrt(4-x^2)+4sin^(-1)(x/2)]_1^2`
`=[(-sqrt3+4sin^(-1)(-1/2))-4sin^(-1)(-1)]+[4sin^(-1)1-sqrt3-4sin^(-1)(1/2)]`
`=[(-sqrt3-4xxpi/6)+4xxpi/2]+[4xxpi/2-sqrt3-4xxpi/6]`
`=(8pi)/3-2sqrt3`
APPEARS IN
RELATED QUESTIONS
Find the slope of the tangent to the curve y = (x -1)/(x - 2), x != 2 at x = 10.
The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(A) (1, 2)
(B) (2, 1)
(C) (1, −2)
(D) (−1, 2)
Find the slope of the tangent and the normal to the following curve at the indicted point x = a (θ − sin θ), y = a(1 − cos θ) at θ = −π/2 ?
At what point of the curve y = x2 does the tangent make an angle of 45° with the x-axis?
Find the equation of the tangent and the normal to the following curve at the indicated point y = x2 at (0, 0) ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[y^2 = \frac{x^3}{4 - x}at \left( 2, - 2 \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \text { at } \left( a\sec\theta, b\tan\theta \right)\] ?
Find the equation of the tangent to the curve x = θ + sin θ, y = 1 + cos θ at θ = π/4 ?
Find the equation of the tangent and the normal to the following curve at the indicated points \[x = \frac{2 a t^2}{1 + t^2}, y = \frac{2 a t^3}{1 + t^2}\text { at } t = \frac{1}{2}\] ?
Find the equation of the tangent line to the curve y = x2 − 2x + 7 which perpendicular to the line 5y − 15x = 13. ?
Find the equation of the tangent to the curve x2 + 3y − 3 = 0, which is parallel to the line y= 4x − 5 ?
Find the angle of intersection of the following curve y2 = x and x2 = y ?
Find the angle of intersection of the following curve x2 + y2 = 2x and y2 = x ?
Show that the curves 4x = y2 and 4xy = k cut at right angles, if k2 = 512 ?
Write the coordinates of the point on the curve y2 = x where the tangent line makes an angle \[\frac{\pi}{4}\] with x-axis ?
Write the slope of the normal to the curve \[y = \frac{1}{x}\] at the point \[\left( 3, \frac{1}{3} \right)\] ?
The equation of the normal to the curve y = x + sin x cos x at x = `π/2` is ___________ .
The angle between the curves y2 = x and x2 = y at (1, 1) is ______________ .
At what point the slope of the tangent to the curve x2 + y2 − 2x − 3 = 0 is zero
If the line y = x touches the curve y = x2 + bx + c at a point (1, 1) then _____________ .
The angle of intersection of the curves y = 2 sin2 x and y = cos 2 x at \[x = \frac{\pi}{6}\] is ____________ .
The equation of the normal to the curve y = sinx at (0, 0) is ______.
Find an angle θ, 0 < θ < `pi/2`, which increases twice as fast as its sine.
The two curves x3 – 3xy2 + 2 = 0 and 3x2y – y3 – 2 = 0 intersect at an angle of ______.
At (0, 0) the curve y = x3 + x
If `tan^-1x + tan^-1y + tan^-1z = pi/2`, then
Let `y = f(x)` be the equation of the curve, then equation of normal is
The number of values of c such that the straight line 3x + 4y = c touches the curve `x^4/2` = x + y is ______.
The normals to the curve x = a(θ + sinθ), y = a(1 – cosθ) at the points θ = (2n + 1)π, n∈I are all ______.
