Question

The area of the region bounded by the parabola (y − 2)² = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .

पर्याय

• 3

• 6

• 7

• none of these

Answer 1

none of these

 

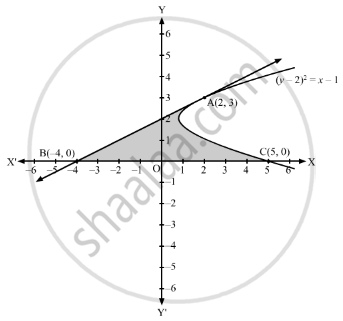
The tangent passes through the point with ordinate 3, so substituting y = 3 in equation of parabola (y − 2)² = x − 1, we get x = 2
Therefore, the line touches the parabola at (2, 3).
We have,
\[\left( y - 2 \right)^2 = x - 1\]
\[ \Rightarrow y - 2 = \sqrt{x - 1}\]
\[ \Rightarrow y = \sqrt{x - 1} + 2\]
Slope of the tangent of parabola at x = 2

\[\left[ \frac{d y}{d x} \right]_{x = 2} = \left[ \frac{1}{2\sqrt{x - 1}} \right]_{x = 2} = \frac{1}{2}\]
Therefore, the equation of the tangent is given as: 
\[y - y_0 = m\left( x - x_0 \right)\]
\[ \Rightarrow y - 3 = \frac{1}{2}\left( x - 2 \right)\]
\[ \Rightarrow y = \frac{1}{2}x + 2\]
Therefore, area of the required region ABC,
\[A = \int_0^3 \left( x_1 - x_2 \right) dy ...........\left[\text{Where, }x_1 = \left( y - 2 \right)^2 + 1\text{ and }x_2 = 2\left( y - 2 \right) \right]\]
\[ = \int_0^3 \left( x_1 - x_2 \right) d y\]
\[ = \int_0^3 \left( y - 2 \right)^2 + 1 - 2\left( y - 2 \right) d y\]
\[ = \int_0^3 \left[ \left( y - 2 \right) - 1 \right]^2 d y\]
\[ = \int_0^3 \left[ y - 3 \right]^2 d y\]
\[ = \left[ \frac{\left( y - 3 \right)^3}{3} \right]_0^3 \]
\[ = \left[ \frac{\left( 3 - 3 \right)^3}{3} \right] - \left[ \frac{\left( 0 - 3 \right)^3}{3} \right]\]
\[ = 9\]