Advertisements
Advertisements
प्रश्न
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
उत्तर
`x^2+y^2=9 and y^2=8x`
`x^2+8x=9`
`x^2+8x-9=0`
`therefore (x+9)(x-1)=0`
`therefore x=1 or x=-9 `
`therefore y=+-2sqrt2`
∴ The points of intersections are
`P(1,2sqrt2) and Q(1,-2sqrt2)`
`y^2=8x`
`therefore y=sqrt8sqrtx=2sqrt2 x^(1/2)-> f_1(x)`
`and x^2+y^2=9 therefore y^2=9-x^2`
`therefore y=sqrt(9-x^2)-> f_2(x)`
Required area,
= Area OPAQO = 2 Area OPAMO
= 2(Area OPMO + Area APMA)
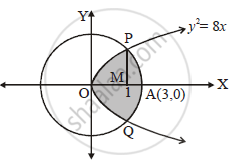
`=2[int_0^1f_1(x)dx+int_1^3f_2(x)dx]`
`=2[int_0^12sqrt2 x^(1/2)dx+int_1^3sqrt(9-x^2)dx]`
`=2[2sqrt2(x^(3/2)/(3/2))_0^1+(x/2sqrt(9-x^2)+9/2sin^-1(x/3)_1^3)]`
`=2[(4sqrt2)/3+(3/2(0)+9/2sin^-1 (1)-1/2sqrt8-9/2sin^-1 (1/3))]`
`=2[(4sqrt2)/3+9/2.x/2-sqrt2-9/2sin^-1 (1/3)]`
`=2[(sqrt2/3+(9pi)/4-9/2 sin^-1 (1/3)) sq. units`
APPEARS IN
संबंधित प्रश्न
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region bounded by y = | x − 1 | and y = 1.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.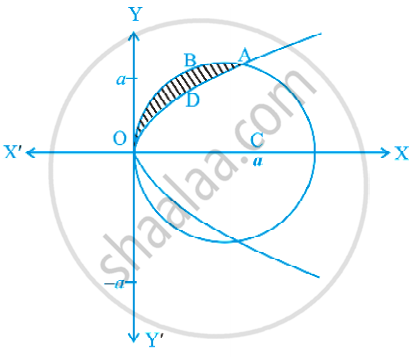
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
The area bounded by `y`-axis, `y = cosx` and `y = sinx, 0 ≤ x - (<pi)/2` is
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
Area of figure bounded by straight lines x = 0, x = 2 and the curves y = 2x, y = 2x – x2 is ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
