Advertisements
Advertisements
प्रश्न
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
उत्तर
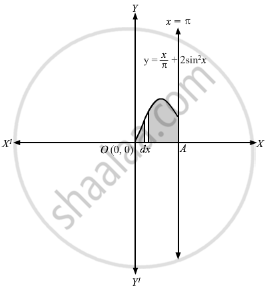
The table for different values of x and y is
| X | 0 | `pi/6` | `pi/2` | `(5pi)/6` | `pi` |
| sin x | 0 | `1/2` | 1 | `1/2` | 0 |
| \[y = \frac{\pi}{2} + 2 \sin^2 x\] | 0 | `2/3` | `5/2` | `4/3` | 1 |
\[y = \frac{x}{\pi} + 2 \sin^2 x ,\text{ is an arc cutting }y -\text{ axis at O(0, 0) and cutting }x = \pi \text{ at } \left( \pi, 1 \right)\]
\[\text{ Consider a vertical strip of length }= \left| y \right| \text{ and width }= dx \text{ in the first quadrant }\]
\[ \therefore\text{ Area of approximating rectangle }= \left| y \right| dx\]
\[\text{ The approximating rectangle moves from }x = 0\text{ to }x = \pi\]
\[ \Rightarrow\text{ Area of the shaded area }= \int_0^\pi \left| y \right| dx\]
\[ \Rightarrow A = \int_0^\pi y dx ..............\left\{ As, y > 0 \Rightarrow \left| y \right| = y \right\}\]
\[ \Rightarrow A = \int_0^\pi \left( \frac{x}{\pi} + 2 \sin^2 x \right) dx\]
\[ \Rightarrow A = \frac{1}{\pi} \int_0^\pi x dx + 2 \int_0^\pi \sin^2 x dx\]
\[ \Rightarrow A = \frac{1}{\pi} \left[ \frac{x^2}{2} \right]_0^\pi + 2 \left[ \frac{x}{2} - \frac{1}{2}\sin x \cos x \right]_0^\pi \]
\[ \Rightarrow A = \frac{\pi^2}{2\pi} + \frac{2}{2}\left[ \pi - \frac{1}{2}\sin \pi \cos \pi - 0 \right]\]
\[ \Rightarrow A = \frac{\pi}{2} + \pi\]
\[ \Rightarrow A = \frac{3\pi}{2}\text{ sq . units }\]
\[ \therefore\text{ Area of the curve enclosed between }x = 0\text{ and }x = \pi\text{ is }\frac{3\pi}{2}\text{ sq . units }\]
APPEARS IN
संबंधित प्रश्न
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x − x2 and y = x2− x?
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area bounded by the parabola y2 = 4ax, latusrectum and x-axis is ___________ .
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.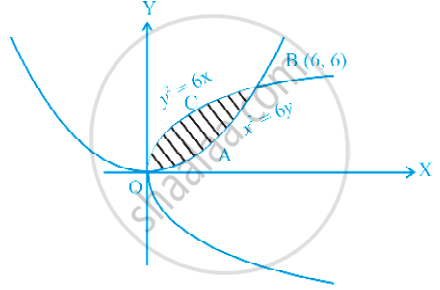
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.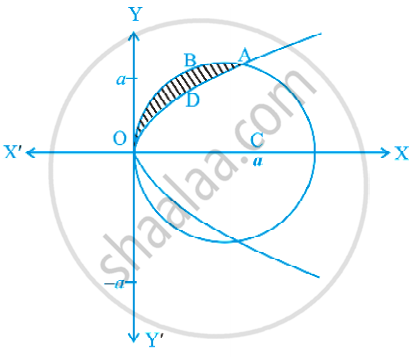
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Hence find the area bounded by the curve, y = x |x| and the coordinates x = −1 and x = 1.
