Advertisements
Advertisements
प्रश्न
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
उत्तर
Let ABC be the triangle with vertices A(−1, 2), B(1, 5) and C(3, 4).
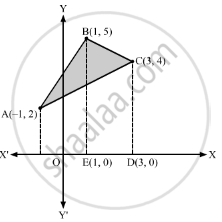
Equation of AB is \[y - 5 = \left( \frac{2 - 5}{- 1 - 1} \right)\left( x - 1 \right)\]
\[ \Rightarrow y - 5 = \frac{3}{2}\left( x - 1 \right)\]
\[ \Rightarrow y = \frac{3}{2}x + 5 - \frac{3}{2} = \frac{3x + 7}{2}\]
Equation of BC is \[y - 4 = \left( \frac{5 - 4}{1 - 3} \right)\left( x - 3 \right)\]
\[ \Rightarrow y - 4 = - \frac{1}{2}\left( x - 3 \right)\]
\[ \Rightarrow y = - \frac{1}{2}x + 4 + \frac{3}{2} = \frac{- x + 11}{2}\]
Equation of CA is \[y - 2 = \left( \frac{4 - 2}{3 + 1} \right)\left( x + 1 \right)\]
\[ \Rightarrow y - 2 = \frac{1}{2}\left( x + 1 \right)\]
\[ \Rightarrow y = \frac{1}{2}x + 2 + \frac{1}{2} = \frac{x + 5}{2}\]
∴ Required area = Area of the shaded region
= Area of the region ABEFA + Area of the region BCDEB − Area of the region ACDFA
\[= \int_{- 1}^1 y_{AB} dx + \int_1^3 y_{BC} dx - \int_{- 1}^3 y_{CA} dx\]
\[ = \int_{- 1}^1 \left( \frac{3x + 7}{2} \right)dx + \int_1^3 \left( \frac{- x + 11}{2} \right)dx - \int_{- 1}^3 \left( \frac{x + 5}{2} \right)dx\]
\[ = \left.\frac{1}{2} \times \frac{\left( 3x + 7 \right)^2}{2 \times 3}\right|_{- 1}^1 + \left.\frac{1}{2} \times \frac{\left( - x + 11 \right)^2}{2 \times \left( - 1 \right)}\right|_1^3 - \left.\frac{1}{2} \times \frac{\left( x + 5 \right)^2}{2}\right|_{- 1}^3 \]
\[ = \frac{1}{12}\left( 100 - 16 \right) - \frac{1}{4}\left( 64 - 100 \right) - \frac{1}{4}\left( 64 - 16 \right)\]
\[ = \frac{84}{12} + \frac{36}{4} - \frac{48}{4}\]
\[ = 7 + 9 - 12\]
\[ = 4\text{ square units }\]
APPEARS IN
संबंधित प्रश्न
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Draw a rough sketch of the curve and find the area of the region bounded by curve y2 = 8x and the line x =2.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Make a rough sketch of the graph of the function y = 4 − x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x-axis and the lines x = 0 and x = 2.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Sketch the graph y = | x + 3 |. Evaluate \[\int\limits_{- 6}^0 \left| x + 3 \right| dx\]. What does this integral represent on the graph?
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x − x2 and y = x2− x?
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
