Question

Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4). 

Answer 1

Let ABC be the triangle with vertices A(−1, 2), B(1, 5) and C(3, 4).

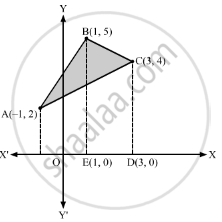
Equation of AB is \[y - 5 = \left( \frac{2 - 5}{- 1 - 1} \right)\left( x - 1 \right)\]
\[ \Rightarrow y - 5 = \frac{3}{2}\left( x - 1 \right)\]
\[ \Rightarrow y = \frac{3}{2}x + 5 - \frac{3}{2} = \frac{3x + 7}{2}\]
Equation of BC is  \[y - 4 = \left( \frac{5 - 4}{1 - 3} \right)\left( x - 3 \right)\]
\[ \Rightarrow y - 4 = - \frac{1}{2}\left( x - 3 \right)\]
\[ \Rightarrow y = - \frac{1}{2}x + 4 + \frac{3}{2} = \frac{- x + 11}{2}\]
Equation of CA is  \[y - 2 = \left( \frac{4 - 2}{3 + 1} \right)\left( x + 1 \right)\]
\[ \Rightarrow y - 2 = \frac{1}{2}\left( x + 1 \right)\]
\[ \Rightarrow y = \frac{1}{2}x + 2 + \frac{1}{2} = \frac{x + 5}{2}\]
∴ Required area = Area of the shaded region
                           = Area of the region ABEFA + Area of the region BCDEB − Area of the region ACDFA
\[= \int_{- 1}^1 y_{AB} dx + \int_1^3 y_{BC} dx - \int_{- 1}^3 y_{CA} dx\]
\[ = \int_{- 1}^1 \left( \frac{3x + 7}{2} \right)dx + \int_1^3 \left( \frac{- x + 11}{2} \right)dx - \int_{- 1}^3 \left( \frac{x + 5}{2} \right)dx\]
\[ = \left.\frac{1}{2} \times \frac{\left( 3x + 7 \right)^2}{2 \times 3}\right|_{- 1}^1 + \left.\frac{1}{2} \times \frac{\left( - x + 11 \right)^2}{2 \times \left( - 1 \right)}\right|_1^3 - \left.\frac{1}{2} \times \frac{\left( x + 5 \right)^2}{2}\right|_{- 1}^3 \]
\[ = \frac{1}{12}\left( 100 - 16 \right) - \frac{1}{4}\left( 64 - 100 \right) - \frac{1}{4}\left( 64 - 16 \right)\]
\[ = \frac{84}{12} + \frac{36}{4} - \frac{48}{4}\]
\[ = 7 + 9 - 12\]
\[ = 4\text{ square units }\]