Advertisements
Advertisements
प्रश्न
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
उत्तर
Some points on the graph of y = sin x are as follows. The graph is obtained by joining these points with a curve.
| x | 0 | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `(5pi)/6` | `(3pi)/4` | `(2pi)/3` | `pi` |
| y | 0 | 0.5 | 0.7 | 0.8 | 1 | 0.5 | 0.7 | 0.8 | 0 |
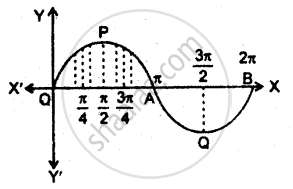
Area of the required region
= Area of the region bounded by the curve OPAQB and the x-axis
= Area of sector OPA + Area of sector AOB
= 2 Area of sector OPA
`= 2 int_0^pi sin x dx`
`= 2 [- cos x]_0^pi`
= 2[1 + 1]
= 2 × 2
= 4 square unit
APPEARS IN
संबंधित प्रश्न
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Find the area common to the circle x2 + y2 = 16 a2 and the parabola y2 = 6 ax.
OR
Find the area of the region {(x, y) : y2 ≤ 6ax} and {(x, y) : x2 + y2 ≤ 16a2}.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area bounded by the parabola y2 = 4ax, latusrectum and x-axis is ___________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of the region included between y2 = 9x and y = x
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤ `pi/2` is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
