Advertisements
Advertisements
प्रश्न
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
उत्तर
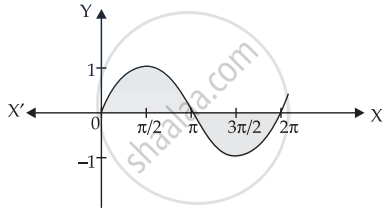
Required area = `int_0^pi sinx "d"x + int_pi^(2pi) |sin x|"d"x`
= `-[cos x]_0^pi + |(- cos x)|_pi^(2pi)`
= `=[cos pi - cos 0] + [cos 2pi - cos pi]`
= `-[-1 - 1] + [1 + 1]`
= 2 + 2
= 4 sq.units
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
