Advertisements
Advertisements
प्रश्न
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
पर्याय
- \[\frac{16}{3}\]
- \[\frac{23}{3}\]
- \[\frac{32}{3}\]
- \[\frac{16\sqrt{2}}{3}\]
उत्तर
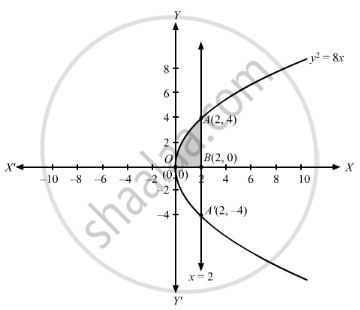
y2 = 8x represents a parabola opening side ways , with vertex at O(0, 0) and Focus at B(2, 0)
Thus AA' represents the latus rectum of the parabola.
The points of intersection of the parabola and latus rectum are A(2, 4) and A'(2, −4)
Area bound by curve , x-axis and latus rectum is the area OABO,
\[\text{ The approximating rectangle of width = dx and length }= \left| y \right| \text{ has area }= \left| y \right| dx,\text{ and moves from }x = 0\text{ to }x = 2\]
\[\text{ area }\left( OABO \right) = \int_0^2 \left| y \right| dx\]
\[ = \int_0^2 y dx ............\left\{ y > 0 , \Rightarrow \left| y \right| = y \right\}\]
\[ = \int_0^2 \sqrt{8x}dx\]
\[ = 2\sqrt{2} \int_0^2 \sqrt{x}dx\]
\[ = 2\sqrt{2} \left[ \frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^2 \]
\[ = 2\sqrt{2} \times \frac{2}{3}\left( 2^\frac{3}{2} - 0 \right)\]
\[ = 4\frac{\sqrt{2}}{3} \times 2\sqrt{2}\]
\[ = \frac{16}{3} \text{ sq units }\]
APPEARS IN
संबंधित प्रश्न
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
Find the equation of the standard ellipse, taking its axes as the coordinate axes, whose minor axis is equal to the distance between the foci and whose length of the latus rectum is 10. Also, find its eccentricity.
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.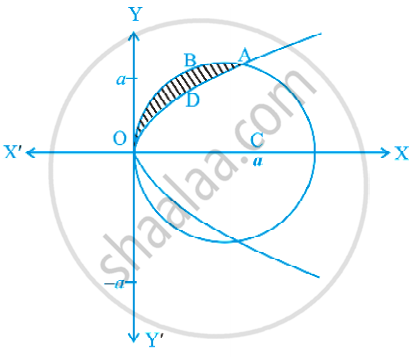
Find the area of the region included between y2 = 9x and y = x
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
