Advertisements
Advertisements
प्रश्न
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
उत्तर
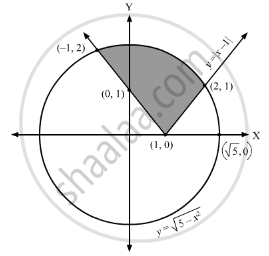
\[\left| x - 1 \right| \leq y \leq \sqrt{5 - x^2}\]
\[\left| x - 1 \right| = \sqrt{5 - x^2}\]
\[x = 2, - 1\]
\[A = \int_{- 1}^2 \left( \sqrt{5 - x^2} - \left| x - 1 \right| \right)dx\]
\[ = \int_{- 1}^2 \sqrt{5 - x^2} + \int_{- 1}^1 \left( x - 1 \right)dx + \int_1^2 \left( 1 - x \right)dx\]
\[ = \left[ \frac{x}{2}\sqrt{5 - x^2} + \frac{5}{2} \sin^{- 1} \left( \frac{x}{\sqrt{5}} \right) \right]_{- 1}^2 + \left[ \frac{x^2}{2} - x \right]_{- 1}^1 + \left[ x - \frac{x^2}{2} \right]_1^2 \]
\[ = \frac{5}{2}\left( \sin^{- 1} \left( \frac{2}{\sqrt{5}} \right) + \sin^{- 1} \left( \frac{1}{\sqrt{5}} \right) \right) + \frac{1}{2}\]
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the curve y = sinx, the lines x=-π/2 , x=π/2 and X-axis
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the equation of the standard ellipse, taking its axes as the coordinate axes, whose minor axis is equal to the distance between the foci and whose length of the latus rectum is 10. Also, find its eccentricity.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
