Advertisements
Advertisements
प्रश्न
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
उत्तर
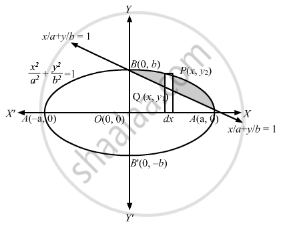
\[\text{ Let }R = \left\{ \left( x, y \right) : \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
\[ \Rightarrow R_1 = \left\{ \left( x, y \right) : \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \right\}\]
\[\text{ and }R_{2 =} \left\{ \left( x, y \right) : 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Then,
\[R = R_1 \cap R_2 \]
\[\text{ Consider }\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 . \text{ This represents an ellipse, symmetrical about both axis and cutting }x - \text{ axis at A(a, 0) and A'( - a, 0) and }y - \text{ axis at B(0, b), B'(0, - b)}\]
\[ \Rightarrow R_1 = \left( \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \right)\text{ represents the area inside the ellipse }\]
\[\frac{x}{a} + \frac{y}{b} = 1 = \text{ represents a straight line cutting }x - \text{ axis at A(a, 0) and }y - \text{ axis at B(0, b)}\]
\[ \Rightarrow R_2 = \left( \frac{x}{a} + \frac{y}{b} \geq 1 \right)\text{ represents the area above the straight line }\]
\[ \Rightarrow R = R_1 \cap R_2\text{ represents the smaller shaded area bounded by the line and the ellipse }\]
\[\text{ In the shaded region, consider a vertical strip with length }= \left| y_2 - y_1 \right|\text{ and width = dx, such that }P(x, y_2 ) \text{ lies on ellipse and }Q(x, y_1 )\text{ lies on the straight line }\]
\[\text{ Area of approximating rectangle }= \left| y_2 - y_1 \right| dx \]
\[\text{ The approximating rectangle moves from }x = 0\text{ to }x = a\]
\[ \therefore \text{ Area of the shaded region }= \int_0^a \left| y_2 - y_1 \right| dx = \int_0^a \left( y_2 - y_1 \right) dx ..................\left[ As, y_2 > y_1 , \left| y_2 - y_1 \right| = y_2 - y_1 \right] \]
\[ \Rightarrow A = \int_0^a \left( \frac{b}{a}\sqrt{a^2 - x^2} - \frac{b}{a}\left( a - x \right) \right) dx\]
\[ \Rightarrow A = \int_0^a \left( \frac{b}{a}\sqrt{a^2 - x^2} \right)dx - \int_0^a \frac{b}{a}\left( a - x \right) dx\]
\[ \Rightarrow A = \frac{b}{a} \left[ \left\{ \frac{x}{2}\sqrt{a^2 - x^2} + \frac{1}{2} a^2 \sin^{- 1} \left( \frac{x}{a} \right) \right\} \right]_0^a - \frac{b}{a}\left[ ax - \frac{x^2}{2} \right]\]
\[ \Rightarrow A = \frac{b}{a}\left[ 0 + \frac{1}{2} a^2 \sin^{- 1} 1 - \left( a^2 - \frac{a^2}{2} \right) \right]\]
\[ \Rightarrow A = \frac{b}{a}\left[ \frac{1}{2} a^2 \times \frac{\pi}{2} - \frac{a^2}{2} \right]\]
\[ \Rightarrow A = \frac{ab}{2}\left[ \frac{\pi}{2} - 1 \right]\]
\[ \Rightarrow A = \frac{ab}{4}\left[ \pi - 2 \right]\text{ sq . units } \]
APPEARS IN
संबंधित प्रश्न
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
If the area enclosed by the parabolas y2 = 16ax and x2 = 16ay, a > 0 is \[\frac{1024}{3}\] square units, find the value of a.
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Find the area of the region bounded by y = `sqrt(x)` and y = x.
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Evaluate:
`int_0^1x^2dx`
