Question

Using integration, find the area of the region bounded between the line x = 2 and the parabola y² = 8x.

Answer 1

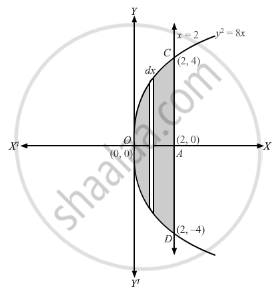
\[y^2 = 8x\text{ represents a parabola with vertex at origin and axis of symmetry along the + ve direction of x - axis}\]
\[x =\text{ 2 is line parallel to y - axis}\]
\[\text{ Let } (x, y)\text{ be a given point on the parabola }, y^2 = 8x\]
\[\text{ Since parabola }y^2 = 8x\text{ is symmetric about x - axis } , \]
\[ \therefore\text{ Required area }= 2 \left(\text{ area OCAO }\right)\]
\[\text{ On slicing the area above x - axis into vertical strips of length }= \left| y \right|\text{ and width }= dx \]
\[ \Rightarrow\text{ area of rectangular strip }= \left| y \right| dx\]
\[\text{The approximating rectangle moves between }x = 0\text{ and }x = 2 . \]
\[\text{ So, area A} = 2 \left(\text{ area OCAO }\right)\]
\[ \Rightarrow A = 2 \int_0^2 \left| y \right| dx = 2 \int_0^2 y dx \text{ as }y > 0 \]
\[ \Rightarrow A = 2 \int_0^2 \sqrt{8x} dx \]
\[ \Rightarrow A = 2 \times 2 \int_0^2 \sqrt{2x} dx = 4\sqrt{2} \int_0^2 \sqrt{x} dx\]
\[ \Rightarrow A = 4\sqrt{2} \left[ \frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^2 = \frac{8}{3}\sqrt{2}\left[ 2^\frac{3}{2} - 0 \right] = \frac{8}{3} \times 2^2 = \frac{32}{3} sq . units\]
\[ \therefore\text{ Area }A = \frac{32}{3}\text{ sq . units}\]