Advertisements
Advertisements
प्रश्न
Draw a rough sketch of the curve y = `sqrt(x - 1)` in the interval [1, 5]. Find the area under the curve and between the lines x = 1 and x = 5.
उत्तर

Here, we have y = `sqrt(x - 1)`
⇒ y2 = x – 1 ......(Parabola)
Area of the required region
= `int_1^5 sqrt(x - 1) "d"x`
= `2/3 [(x - 1)^(3/2)]_1^5`
= `2/3 [(5 - 1)^(3/2) - 0]`
= `2/3 xx (4)^(2/3)`
= `2/3 xx 8`
= `16/3` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region lying between the parabolas y2 = 4ax and x2 = 4ay.
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3
Using integration find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.
Using the method of integration find the area bounded by the curve |x| + |y| = 1 .
[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and
– x – y = 1].
Choose the correct answer The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
A. `4/3 (4pi - sqrt3)`
B. `4/3 (4pi + sqrt3)`
C. `4/3 (8pi - sqrt3)`
D.`4/3 (4pi + sqrt3)`
The area bounded by the y-axis, y = cos x and y = sin x when 0 <= x <= `pi/2`
(A) 2 ( 2 −1)
(B) `sqrt2 -1`
(C) `sqrt2 + 1`
D. `sqrt2`
Using integration, find the area of region bounded by the triangle whose vertices are (–2, 1), (0, 4) and (2, 3).
Find the area included between the parabolas y2 = 4ax and x2 = 4by.
Solve the following :
Find the area of the region lying between the parabolas :
y2 = 4x and x2 = 4y
The area of the region included between the parabolas y2 = 16x and x2 = 16y, is given by ______ sq.units
Find the area of sector bounded by the circle x2 + y2 = 25, in the first quadrant−
Find the area enclosed between the X-axis and the curve y = sin x for values of x between 0 to 2π
Find the area of the region lying between the parabolas 4y2 = 9x and 3x2 = 16y
Find the area of the region included between y = x2 + 5 and the line y = x + 7
Find the area enclosed between the circle x2 + y2 = 9, along X-axis and the line x = y, lying in the first quadrant
Find the area enclosed by the curve x = 3 cost, y = 2 sint.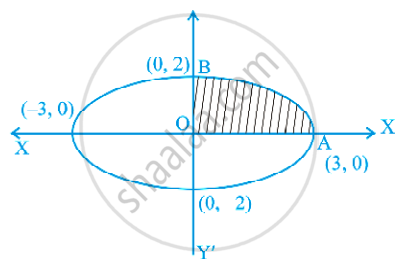
Find the area of the region included between the parabola y = `(3x^2)/4` and the line 3x – 2y + 12 = 0.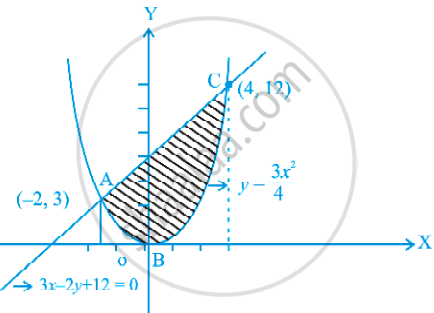
Find the area of the region bounded by the curves x = at2 and y = 2at between the ordinate corresponding to t = 1 and t = 2.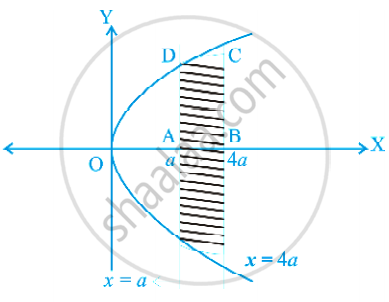
Find the area of a minor segment of the circle x2 + y2 = a2 cut off by the line x = `"a"/2`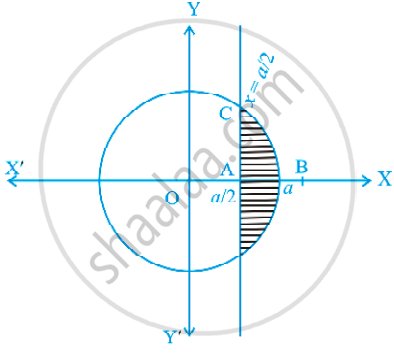
Calcualte the area under the curve y = `2sqrt(x)` included between the lines x = 0 and x = 1
The value of a for which the area between the curves y2 = 4ax and x2 = 4ay is 1 sq.unit, is ______.
Using Integration, find the area of triangle whose vertices are (– 1, 1), (0, 5) and (3, 2).
Find the area cut off from the parabola 4y = 3x2 by the line 2y = 3x + 12.
