Advertisements
Advertisements
प्रश्न
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
उत्तर
We have Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`
Interchanging rows and columns, we get
Δ1 = `|(1, yz, x),(1, z, y),(1, xy, z)|`
= `1/(xyz) |(x, xyz, x^2),(y, xyz, y^2),(z, xyz, z^2)|`
= `(xyz)/(xyz) |(x, 1, x^2),(y, 1, y^2),(z, 1, z^2)|`
Interchanging C1 and C2
= `(-1)|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`
= – Δ
⇒ Δ1 + Δ = 0
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find equation of line joining (1, 2) and (3, 6) using the determinant.
Find equation of line joining (3, 1) and (9, 3) using determinant.
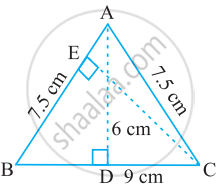
ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
For what value of x are the points A(-3, 12), B(7, 6) and C(x, 9) collinear.
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
If the centroid of ΔABC having vertices A (a,b) , B (b,c) and C (c,a) is the origin, then find the value of (a+b+c).
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
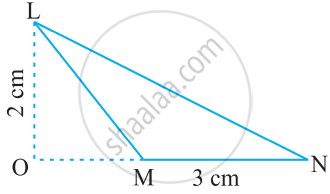
Find the area of the following triangle:
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 5 feet | ? | 20 sq.feet |
The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq.units. The value of k will be ______.
The points (0, 5), (0, –9) and (3, 6) are collinear.
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
Find the missing value:
| Base | Height | Area of Triangle |
| ______ | 31.4 mm | 1256 mm2 |
