Advertisements
Advertisements
प्रश्न
The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq.units. The value of k will be ______.
विकल्प
9
±3
– 9
6
उत्तर
The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq.units. The value of k will be ±3.
Explanation:
We know that, area of triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is given by
Δ = `1/2|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|`
∴ Area of triangle with verticles (–3, 0), (3, 0) and (0, k) is
∴ Δ = `1/2|(-3, 0, 1),(3, 0, 1),(0, "k", 1)|` = 9 ...(Given)
⇒ `[-3(-"k") - 0 + 1(3"k")]` = ±18
⇒ 6k = ±18
∴ k = `+- 18/6` = ±3
संबंधित प्रश्न
If the points A(−1, −4), B(b, c) and C(5, −1) are collinear and 2b + c = 4, find the values of b and c.
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
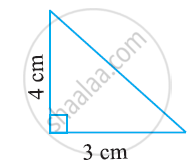
Find the area of the following triangle:
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

Prove that (2, -2) (-2, 1) and (5, 2) are the vertices of a right-angled triangle. Find the area of the triangle and the length of the hypotenuse.
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
A(6,1) , B(8,2) and C(9,4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
Points A(3, 1), B(12, –2) and C(0, 2) cannot be the vertices of a triangle.
The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

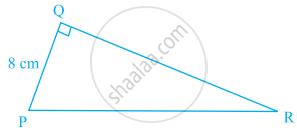
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
