Advertisements
Advertisements
प्रश्न
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
उत्तर
| Base | Height | Area of triangle |
| 15 cm | 11.6 | 87 cm2 |
Explanation:
Area of Triangle = `1/2 xx "Base" xx "Height"`
b = 15 cm
h = ?
Area = `1/2 xx b xx h` = 87 cm2
`1/2 xx 15 xx h` = 87 cm2
h = `(87xx 2)/15`
h = 11.6 cm
Therefore, the height of triangle is 11.6 cm.
APPEARS IN
संबंधित प्रश्न
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
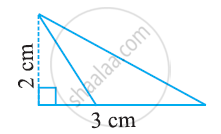
Find the area of the following triangle:
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
For what value of x are the points A(-3, 12), B(7, 6) and C(x, 9) collinear.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 15 cm | 154.5 cm2 |
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
