Advertisements
Advertisements
प्रश्न
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
विकल्प
2Δ2
4Δ2
2Δ
4Δ
उत्तर
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to 4Δ2.
Explanation:
If (a, b), (c, d) and (e, f) are vertices of ΔABC, then its area is
Δ = `1/2|(a, b, 1),(c, d, 1),(e, f, 1)|`
Δ = `1/2|(a, c ,e),(b, d, f),(1, 1, 1)|`
2Δ = `|(a, c, e),(b, d, f),(1, 1, 1)|`
On squaring both sides, we get
`\implies` (2Δ)2 = `|(a, c, e),(b, d, f),(1, 1, 1)|^2`
∴ `|(a, c, e),(b, d, f),(1, 1, 1)|^2` = 4Δ2.
APPEARS IN
संबंधित प्रश्न
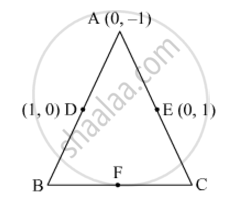
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Find the area of the following triangle:
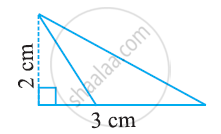
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Prove that (2, -2) (-2, 1) and (5, 2) are the vertices of a right-angled triangle. Find the area of the triangle and the length of the hypotenuse.
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
If `a≠ b ≠ c`, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
Find the value of p for which the points (−5, 1), (1, p) and (4, −2) are collinear.
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
If `D((-1)/2, 5/2), E(7, 3)` and `F(7/2, 7/2)` are the midpoints of sides of ∆ABC, find the area of the ∆ABC.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

