Advertisements
Advertisements
Question
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
Options
2Δ2
4Δ2
2Δ
4Δ
Solution
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to 4Δ2.
Explanation:
If (a, b), (c, d) and (e, f) are vertices of ΔABC, then its area is
Δ = `1/2|(a, b, 1),(c, d, 1),(e, f, 1)|`
Δ = `1/2|(a, c ,e),(b, d, f),(1, 1, 1)|`
2Δ = `|(a, c, e),(b, d, f),(1, 1, 1)|`
On squaring both sides, we get
`\implies` (2Δ)2 = `|(a, c, e),(b, d, f),(1, 1, 1)|^2`
∴ `|(a, c, e),(b, d, f),(1, 1, 1)|^2` = 4Δ2.
APPEARS IN
RELATED QUESTIONS
Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
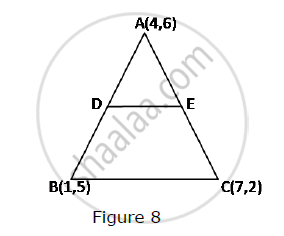
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
If the points A(x, 2), B(−3, −4) and C(7, − 5) are collinear, then the value of x is:
(A) −63
(B) 63
(C) 60
(D) −60
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4), then k is ______.
Find the area of the following triangle:

ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
For what value of a point (a, 1), (1, -1) and (11, 4) are collinear?
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
Find a relation between x and y, if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

Find the area of the following triangle:

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points A(–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
If area of a triangular piece of cardboard is 90 cm2, then the length of altitude corresponding to 20 cm long base is ______ cm.
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
