Advertisements
Advertisements
Question
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
Options
14
28
8
6
Solution
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is 8.
Explanation:
Vertices of the triangle are,
A(x1, y1) = (3, 0)
B(x2, y2) = (7, 0)
C(x3, y3) = (8, 4)
Area of triangle = `|1/2[x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)]|`
= `|1/2[3(0 - 4) + 7(4 - 0) + 8(0 - 0)]|`
= `|1/2[-12 + 28 + 0]|`
= `|1/2[16]|`
= 8
Therefore, the area of ΔABC is 8.
APPEARS IN
RELATED QUESTIONS
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
Prove that the points (2, – 2), (–3, 8) and (–1, 4) are collinear
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
Find the area of the quadrilaterals, the coordinates of whose vertices are
(−3, 2), (5, 4), (7, −6) and (−5, −4)
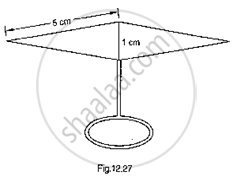
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
Points A(–6, 10), B(–4, 6) and C(3, –8) are collinear such that AB = `2/9` AC.
