Advertisements
Advertisements
Question
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is ______.
Options
5 units
12 units
10 units
11 units
`7 + sqrt(5)` units
Solution
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is 12 units.
Explanation:
The vertices of a triangle are (0, 4), (0, 0) and (3, 0).
Now, perimeter of ΔAOB = Sum of the length of all its sides
= Distance between (OA + OB + AB)
Distance between the points (x1, y1) and (x2, y2) is given by,
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`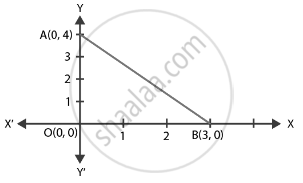
To find:
Distance between A(0, 4) and O(0, 0) + Distance between O(0, 0) and B(3, 0) + Distance between A(0, 4) and B(3, 0)
= `sqrt((0 - 0)^2 + (0 - 4)^2) + sqrt((3 - 0)^2 + (0 - 0)^2) + sqrt((3 - 0)^2 + (0 - 4)^2)`
= `sqrt(0 + 16) + sqrt(9 + 0) + sqrt((3)^2 + (4)^2`
= `4 + 3 + sqrt(9 + 16)`
= `7 + sqrt(25)`
= 7 + 5
= 12
Therefore, the required perimeter of the triangle is 12.
RELATED QUESTIONS
If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also, find the length of AB.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(- 1, - 2), (1, 0), (- 1, 2), (- 3, 0)
ABC is a triangle and G(4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b) and C = (a, 1), find ‘a’ and ‘b’. Find the length of side BC.
Find value of x for which the distance between the points P(x,4) and Q(9,10) is 10 units.
Find the distance between the following pair of point in the coordinate plane :
(5 , -2) and (1 , 5)
Find the distance between the following point :
(sec θ , tan θ) and (- tan θ , sec θ)
Find the relation between a and b if the point P(a ,b) is equidistant from A (6,-1) and B (5 , 8).
Prove that the points (a, b), (a + 3, b + 4), (a − 1, b + 7) and (a − 4, b + 3) are the vertices of a parallelogram.
Calculate the distance between A (7, 3) and B on the x-axis whose abscissa is 11.
Find a point which is equidistant from the points A(–5, 4) and B(–1, 6)? How many such points are there?
