Advertisements
Advertisements
Question
AOBC is a rectangle whose three vertices are A(0, 3), O(0, 0) and B(5, 0). The length of its diagonal is ______.
Options
5
3
`sqrt(34)`
4
Solution
AOBC is a rectangle whose three vertices are A(0, 3), O(0, 0) and B(5, 0). The length of its diagonal is `underlinebb(sqrt(34))`.
Explanation:
The three vertices are: A = (0, 3), O = (0, 0), B = (5, 0)
We know that, the diagonals of a rectangle are of equal length,
Length of the diagonal AB = Distance between the points A and B
Distance formula: d2 = (x2 – x1)2 + (y2 – y1)2
According to the question,
We have,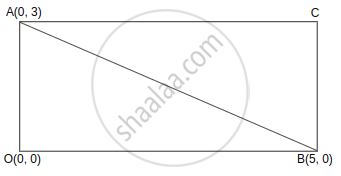
x1 = 0, x2 = 5
y1 = 3, y2 = 0
d2 = (5 – 0)2 + (0 – 3)2
d = `sqrt((5 - 0)^2 + (0 - 3)^2`
d = `sqrt(25 + 9)`
= `sqrt(34)`
Distance between A(0, 3) and B(5, 0) is `sqrt(34)`
Therefore, the length of its diagonal is `sqrt(34)`
APPEARS IN
RELATED QUESTIONS
Prove that the points (–3, 0), (1, –3) and (4, 1) are the vertices of an isosceles right angled triangle. Find the area of this triangle
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.
AB and AC are the two chords of a circle whose radius is r. If p and q are
the distance of chord AB and CD, from the centre respectively and if
AB = 2AC then proove that 4q2 = p2 + 3r2.
Find the distance of the following point from the origin :
(13 , 0)
Find the distance of a point (13 , -9) from another point on the line y = 0 whose abscissa is 1.
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
A point P (2, -1) is equidistant from the points (a, 7) and (-3, a). Find a.
A point P lies on the x-axis and another point Q lies on the y-axis.
Write the abscissa of point Q.
Point P (2, -7) is the center of a circle with radius 13 unit, PT is perpendicular to chord AB and T = (-2, -4); calculate the length of: AT

The points A(–1, –2), B(4, 3), C(2, 5) and D(–3, 0) in that order form a rectangle.
