Advertisements
Advertisements
Question
Prove that the points (–3, 0), (1, –3) and (4, 1) are the vertices of an isosceles right angled triangle. Find the area of this triangle
Sum
Solution
Let A (–3, 0), B (1, –3) and C (4, 1) be the given points. Then,
`AB=sqrt({1-(-3)}^2+(-3-0)^2)=sqrt(16+9)= `
`BC=sqrt((4-1)^2+(1+3)^2)=\sqrt{9+16}=`
`CA=sqrt((4+3)^2+(1-0)^2)=sqrt(49+1)=5\sqrt{2}`
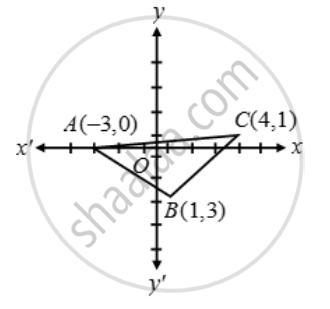
Clearly, AB = BC. Therefore, ∆ABC is isosceles.
Also,
`AB^2 + BC^2 = 25 + 25 = (5)^2 = CA^2`
⇒ ∆ABC is right-angled at B.
Thus, ∆ABC is a right-angled isosceles triangle.
Now,
`Area of ∆ABC = \frac { 1 }{ 2 } (Base × Height)`
`= \frac { 1 }{ 2 } (AB × BC)`
`⇒ Area of ∆ABC = \frac { 1 }{ 2 } × 5 × 5 sq. units`
`= \frac { 25 }{ 2 } sq. units`
shaalaa.com
Is there an error in this question or solution?
