Question

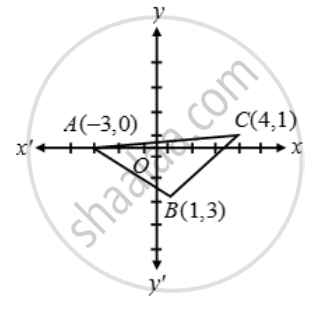
Prove that the points (–3, 0), (1, –3) and (4, 1) are the vertices of an isosceles right angled triangle. Find the area of this triangle

Answer 1

Let A (–3, 0), B (1, –3) and C (4, 1) be the given points. Then,

`AB=sqrt({1-(-3)}^2+(-3-0)^2)=sqrt(16+9)= `

`BC=sqrt((4-1)^2+(1+3)^2)=\sqrt{9+16}=`

`CA=sqrt((4+3)^2+(1-0)^2)=sqrt(49+1)=5\sqrt{2}`

Clearly, AB = BC. Therefore, ∆ABC is isosceles.

Also,

`AB^2 + BC^2 = 25 + 25 = (5)^2 = CA^2`

⇒ ∆ABC is right-angled at B.

Thus, ∆ABC is a right-angled isosceles triangle.

Now,

`Area of ∆ABC = \frac { 1 }{ 2 } (Base × Height)`

`= \frac { 1 }{ 2 } (AB × BC)`

`⇒ Area of ∆ABC = \frac { 1 }{ 2 } × 5 × 5 sq. units`

`= \frac { 25 }{ 2 } sq. units`