Advertisements
Advertisements
Question
The points A(–1, –2), B(4, 3), C(2, 5) and D(–3, 0) in that order form a rectangle.
Options
True
False
Advertisements
Solution
This statement is True.
Explanation:
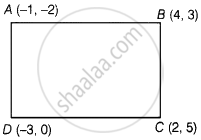
Distance between A(–1, –2), B(4, 3),
AB = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
AB = `sqrt((4 + 1)^2 + (3 + 2)^2`
= `sqrt(5^2 + 5^2)`
= `sqrt(25 + 25)`
= `5sqrt(2)`
Distance between C(2, 5) and D(–3, 0),
CD = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
CD = `sqrt((-3 - 2)^2 + (0 - 5)^2`
= `sqrt((-5)^2 + (-5)^2)`
= `sqrt(25 + 25)`
= `5sqrt(2)`
Distance between A(–1, –2) and D(–3, 0),
AD = `sqrt((-3 + 1)^2 + (0 + 2)^2`
= `sqrt((-2)^2 + 2^2)`
= `sqrt(4 + 4)`
= `2sqrt(2)`
And distance between B(4, 3) and C(2, 5),
BC = `sqrt((4 - 2)^2 + (3 - 5)^2`
= `sqrt(2^2 + (-2)^2)`
= `sqrt(4 + 4)`
= `2sqrt(2)`
We know that, in a rectangle, opposite sides and equal diagonals are equal and bisect each other.
Since, AB = CD and AD = BC
Also, distance between A(–1, –2) and C(2, 5),
AC = `sqrt((2 + 1)^2 + (5 + 2)^2`
= `sqrt(3^2 + 7^2)`
= `sqrt(9 + 49)`
= `sqrt(58)`
And distance between D(–3, 0) and B(4, 3),
DB = `sqrt((4 + 3)^2 + (3 - 0)^2`
= `sqrt(7^2 + 3^2)`
= `sqrt(49 + 9)`
= `sqrt(58)`
Since, diagonals AC and BD are equal.
Hence, the points A(–1, – 2), B(4, 3), C(2, 5) and D(–3, 0) form a rectangle.
APPEARS IN
RELATED QUESTIONS
If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also, find the length of AB.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Determine if the points (1, 5), (2, 3) and (−2, −11) are collinear.
Name the type of quadrilateral formed, if any, by the following point, and give reasons for your answer:
(4, 5), (7, 6), (4, 3), (1, 2)
If the point P(x, y ) is equidistant from the points A(5, 1) and B (1, 5), prove that x = y.
Determine whether the point is collinear.
R(0, 3), D(2, 1), S(3, –1)
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is ______.
Find the distance between the following pairs of point in the coordinate plane :
(13 , 7) and (4 , -5)
Find the relation between x and y if the point M (x,y) is equidistant from R (0,9) and T (14 , 11).
Find the point on the x-axis equidistant from the points (5,4) and (-2,3).
Find the coordinates of O, the centre passing through A( -2, -3), B(-1, 0) and C(7, 6). Also, find its radius.
Prove that the points (7 , 10) , (-2 , 5) and (3 , -4) are vertices of an isosceles right angled triangle.
Prove that the points (a, b), (a + 3, b + 4), (a − 1, b + 7) and (a − 4, b + 3) are the vertices of a parallelogram.
The distance between the points (3, 1) and (0, x) is 5. Find x.
A point P lies on the x-axis and another point Q lies on the y-axis.
Write the ordinate of point P.
If the length of the segment joining point L(x, 7) and point M(1, 15) is 10 cm, then the value of x is ______
Find distance between point A(– 3, 4) and origin O
If the point A(2, – 4) is equidistant from P(3, 8) and Q(–10, y), find the values of y. Also find distance PQ.
Find distance between points P(– 5, – 7) and Q(0, 3).
By distance formula,
PQ = `sqrt(square + (y_2 - y_1)^2`
= `sqrt(square + square)`
= `sqrt(square + square)`
= `sqrt(square + square)`
= `sqrt(125)`
= `5sqrt(5)`
