Advertisements
Advertisements
प्रश्न
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is ______.
पर्याय
5 units
12 units
10 units
11 units
`7 + sqrt(5)` units
Advertisements
उत्तर
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is 12 units.
Explanation:
The vertices of a triangle are (0, 4), (0, 0) and (3, 0).
Now, perimeter of ΔAOB = Sum of the length of all its sides
= Distance between (OA + OB + AB)
Distance between the points (x1, y1) and (x2, y2) is given by,
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`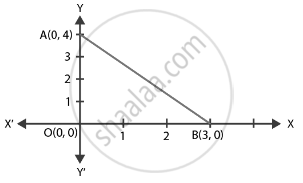
To find:
Distance between A(0, 4) and O(0, 0) + Distance between O(0, 0) and B(3, 0) + Distance between A(0, 4) and B(3, 0)
= `sqrt((0 - 0)^2 + (0 - 4)^2) + sqrt((3 - 0)^2 + (0 - 0)^2) + sqrt((3 - 0)^2 + (0 - 4)^2)`
= `sqrt(0 + 16) + sqrt(9 + 0) + sqrt((3)^2 + (4)^2`
= `4 + 3 + sqrt(9 + 16)`
= `7 + sqrt(25)`
= 7 + 5
= 12
Therefore, the required perimeter of the triangle is 12.
APPEARS IN
संबंधित प्रश्न
Find the distance between the following pairs of points:
(a, b), (−a, −b)
The value of 'a' for which of the following points A(a, 3), B (2, 1) and C(5, a) a collinear. Hence find the equation of the line.
Given a line segment AB joining the points A(–4, 6) and B(8, –3). Find
1) The ratio in which AB is divided by y-axis.
2) Find the coordinates of the point of intersection.
3) The length of AB.
Find the co-ordinates of points of trisection of the line segment joining the point (6, –9) and the origin.
Find the distance between the points
A(-6,-4) and B(9,-12)
Find the distance between the points:
P(a + b, a - b) and Q(a - b, a + b)
Find the distance of the following points from the origin:
(i) A(5,- 12)
Find the distance between the following pair of points.
L(5, –8), M(–7, –3)
Find the distance between the following pairs of point.
W `((- 7)/2 , 4)`, X (11, 4)
Find the distance of a point (12 , 5) from another point on the line x = 0 whose ordinate is 9.
Prove that the points (7 , 10) , (-2 , 5) and (3 , -4) are vertices of an isosceles right angled triangle.
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
PQR is an isosceles triangle . If two of its vertices are P (2 , 0) and Q (2 , 5) , find the coordinates of R if the length of each of the two equal sides is 3.
Find the distance between the following pairs of points:
(–3, 6) and (2, –6)
A point P lies on the x-axis and another point Q lies on the y-axis.
Write the ordinate of point P.
Find distance CD where C(–3a, a), D(a, –2a).
Show that A(1, 2), (1, 6), C(1 + 2`sqrt(3)`, 4) are vertices of an equilateral triangle.
Using distance formula decide whether the points (4, 3), (5, 1) and (1, 9) are collinear or not.
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
Find the value of a, if the distance between the points A(–3, –14) and B(a, –5) is 9 units.
