Advertisements
Advertisements
प्रश्न
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
पर्याय
14
28
8
6
उत्तर
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is 8.
Explanation:
Vertices of the triangle are,
A(x1, y1) = (3, 0)
B(x2, y2) = (7, 0)
C(x3, y3) = (8, 4)
Area of triangle = `|1/2[x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)]|`
= `|1/2[3(0 - 4) + 7(4 - 0) + 8(0 - 0)]|`
= `|1/2[-12 + 28 + 0]|`
= `|1/2[16]|`
= 8
Therefore, the area of ΔABC is 8.
APPEARS IN
संबंधित प्रश्न
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Prove that (2, -2) (-2, 1) and (5, 2) are the vertices of a right-angled triangle. Find the area of the triangle and the length of the hypotenuse.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points A(–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
Ratio of the area of ∆WXY to the area of ∆WZY is 3:4 in the given figure. If the area of ∆WXZ is 56 cm2 and WY = 8 cm, find the lengths of XY and YZ.

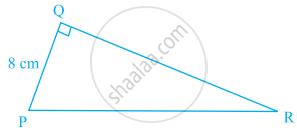
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.