Advertisements
Advertisements
प्रश्न
Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points A(–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
उत्तर
Point Q is the midpoint of AB as the point P lies on the perpendicular bisector of AB.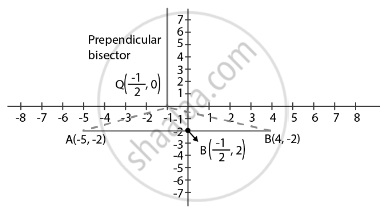
By midpoint formula:
`(x_1 + x_2)/2 = (-5 + 4)/2`
= `-1/2`
x = `-1/2`
Given that,
P lies on x-axis,
So y = 0
P(x, y) = `(-1/2, 0)`
Therefore, it is an isosceles triangle
APPEARS IN
संबंधित प्रश्न
Find the area of the quadrilateral ABCD whose vertices are respectively A(1, 1), B(7, –3), C(12, 2) and D(7, 21).
Prove that the points (2, – 2), (–3, 8) and (–1, 4) are collinear
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
If the points (2, -3), (k, -1), and (0, 4) are collinear, then find the value of 4k.
The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
