Advertisements
Advertisements
Question
Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points A(–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
Solution
Point Q is the midpoint of AB as the point P lies on the perpendicular bisector of AB.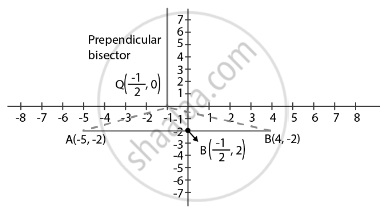
By midpoint formula:
`(x_1 + x_2)/2 = (-5 + 4)/2`
= `-1/2`
x = `-1/2`
Given that,
P lies on x-axis,
So y = 0
P(x, y) = `(-1/2, 0)`
Therefore, it is an isosceles triangle
APPEARS IN
RELATED QUESTIONS
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
