Advertisements
Advertisements
Question
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
Solution
For collinear points, area of triangle formed by them is zero.
Therefore, for points (8, 1), (k, - 4), and (2, - 5), area = 0
`1/2 [8 { -4- (-5)} + k{(-5)-(1)} + 2{1 -(-4)}] = 0`
8 - 6k + 10 = 0
6k = 18
k = 3
APPEARS IN
RELATED QUESTIONS
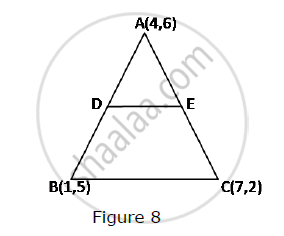
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
For what value of a point (a, 1), (1, -1) and (11, 4) are collinear?
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Find the area of ΔABC with A(1, -4) and midpoints of sides through A being (2, -1) and (0, -1).
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
Find the area of the following triangle:

If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
