Advertisements
Advertisements
Question
Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear.
Solution
The points A(5, 1), B(–2, –3) and C(8, 2m) are collinear.
i.e., Area of ∆ABC = 0
`1/2[x_1 (y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)]` = 0
`1/2[5(-3 - 2m) + (-2)(2m - 1) + 8(1 - (-3))]` = 0
`1/2(-15 - 10m - 4m + 2 + 32)` = 0
`1/2(-14m + 19)` = 0
m = `19/14`
APPEARS IN
RELATED QUESTIONS
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
In the given figure, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is ______.

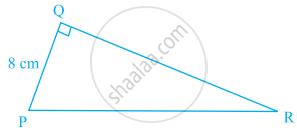
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.