Advertisements
Advertisements
Question
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
Solution
Area of a triangle is given by
Area of triangle = `1/2 {x_1 (y_2 - y_3)+ x_2 (y_3 - y_1)+ x_3 (y_1 - y_2)}`
Area of the given triangle = `1/2 [2 { 0- (-4)} + (-1) {(-4) - (3)} + 2 (3 - 0)]`
`= 1/2 {8 + 7 + 6}`
=`21/2` square units.
APPEARS IN
RELATED QUESTIONS
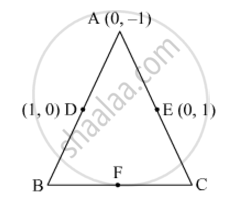
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Find equation of line joining (1, 2) and (3, 6) using the determinant.
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if `1/a+1/b=1`
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
If the points (2, -3), (k, -1), and (0, 4) are collinear, then find the value of 4k.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
