Advertisements
Advertisements
प्रश्न
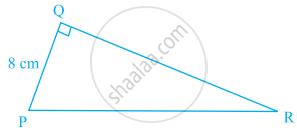
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.
उत्तर
Given, area of ΔPOR = 60 cm2 and side PQ = 8 cm
∴ Area of ΔPQR = `1/2` × PQ × QR ......[∵ Area of triangle = Base × Height]
⇒ 60 = `1/2` × 8 × QR
⇒ QR = `(60 xx 2)/8`
⇒ QR = 15 cm
In right-angled ΔPOR, PR2 + PQ2 + QR2 ......[By Pythagoras theorem]
⇒ PR2 + 82 + 152 = 64 + 225
⇒ PR2 = 289
⇒ PR = `sqrt(289)` = 17 cm
Hence, the length of two sides are 15 cm and 17 cm.
APPEARS IN
संबंधित प्रश्न
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and (5k – 1, 5k) are collinear.
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
Prove that the points (2,3), (-4, -6) and (1, 3/2) do not form a triangle.
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

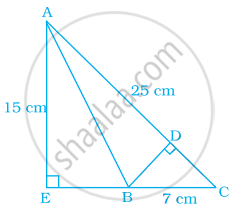
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.