Advertisements
Advertisements
प्रश्न
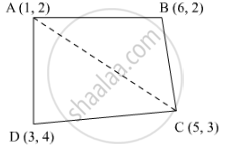
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
उत्तर
Let the vertices of the quadrilateral be A (1, 2), B (6, 2), C (5, 3), and D (3, 4). Join AC to form two triangles ΔABC and ΔACD.
Area of a triangle `=1/2 {x_1(y_2-y_3)+x_2(y_3-y_1)+(y_1-y_2)}`
Area of ΔABC `=1/2 {1(2-3)+6(3-2+5(2-2)}`
`=1/2(-1+6)=5/2` square units
Area of ΔACD `=1/2{1(3-4)+5(4-2)+3(2-3)}`
`=1/2 {-1+10-3}=3` square units
Area of `square`ABCD = Area of ΔABC +Area of ΔACD
`=(5/2+3)` square units = 11/2 square units
APPEARS IN
संबंधित प्रश्न
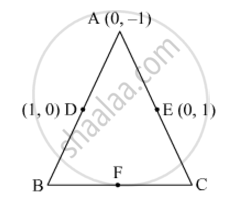
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
Show that ∆ ABC with vertices A (–2, 0), B (0, 2) and C (2, 0) is similar to ∆ DEF with vertices D (–4, 0), F (4, 0) and E (0, 4) ?
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2.
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

