Advertisements
Advertisements
प्रश्न
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
उत्तर
Let the vertices of the quadrilateral be A (1, 2), B (6, 2), C (5, 3), and D (3, 4). Join AC to form two triangles ΔABC and ΔACD.
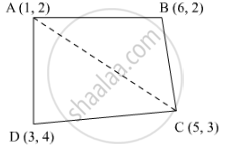
Area of a triangle `=1/2 {x_1(y_2-y_3)+x_2(y_3-y_1)+(y_1-y_2)}`
Area of ΔABC `=1/2 {1(2-3)+6(3-2+5(2-2)}`
`=1/2(-1+6)=5/2` square units
Area of ΔACD `=1/2{1(3-4)+5(4-2)+3(2-3)}`
`=1/2 {-1+10-3}=3` square units
Area of `square`ABCD = Area of ΔABC +Area of ΔACD
`=(5/2+3)` square units = 11/2 square units
APPEARS IN
संबंधित प्रश्न
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
If the points A(x, 2), B(−3, −4) and C(7, − 5) are collinear, then the value of x is:
(A) −63
(B) 63
(C) 60
(D) −60
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the area of the following triangle:

Prove that the points (a, 0), (0, b) and (1, 1) are collinear if `1/a+1/b=1`
If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
If area of a triangular piece of cardboard is 90 cm2, then the length of altitude corresponding to 20 cm long base is ______ cm.
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

Triangles having the same base have equal area.
