Advertisements
Advertisements
प्रश्न
Find the area of the quadrilaterals, the coordinates of whose vertices are
(−3, 2), (5, 4), (7, −6) and (−5, −4)
उत्तर
Let the vertices of the quadrilateral be A (−3, 2), B (5, 4), C (7, −6), and D (−5, −4). Join AC to form two triangles ΔABC and ΔACD.

Area of triangle `=1/2{x_1(y_2-y_3) +x_2(y_3-y_1)+x_3(y_1-y_2)}`
Area of ΔABC `=1/2{-3(4+6)+5(-6-2)+7(2-4)}`
`=1/2(-30-40-14)=-42`
∴ Area of ΔABC = 42 square units
Area of ΔACD `=1/2{-3(-6+4)+7(-4-2)-5(2+6)}`
`=1/2 {6-42-40}=-38`
∴Area of ΔACD =38 square units
Area of `square`ABCD= Area of ΔABC+Area of ΔACD
`=`(42+38) square units =80 square units
APPEARS IN
संबंधित प्रश्न
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Find the area of the following triangle:
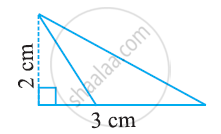
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
The points (0, 5), (0, –9) and (3, 6) are collinear.
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

