Advertisements
Advertisements
प्रश्न
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
उत्तर
We know area of triangle formed by three points (x1y1) , (x2y2), and (x3y3)is given by `triangle=1/2 [x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
The vertices are given as `(at_1^2,2at1),(at_2^2,2at_2),(at_3^2,2at_3)`
`triangle =1/2[at_1^2(2at_2-2at_3)+at_2^2(2at_3-2at_1)+at_3^2(2at_1-2at_2)]`
`=1/2xx2a^2[(t_1^2t_2-t_1^2t_3)+(t_2^2t_3-t_2^2t_1)+(t_3^2t_1-t_3^2t_2)]`
`=a^2[(t_1^2t_2-t_2^2 t_1)+(t_2^2 t_3-t_1^2 t_3)+(t_3^2t_1-t_3^2 t_2)]`
`=a^2 [t_1t_2(t_1-t_2)+t_3 (t_2^2-t_1^2)+t_3^2 (t_1-t_2)]`
`=a^2[(t_1-t_2) {t_1t_2-t_3(t_2+t_1)+t_3^2)]`
`=a^2[(t_1-t_2){t_1t_2-t_3t_2-t_3t_1+t_3^2}`
`=a^2 [(t_1-t_2){t_2(t_1-t_3)-t_3 (-t_3+t_1)}]`
`=a^2[(t_1-t_2) (t_1-t_3)(t_2-t_3)]`
or,`triangle =a_2 (t_1-t_2) (t_2-t_3)(t_3-t_1)` assuming t1> t2, t2 > t3, t3 > t1
APPEARS IN
संबंधित प्रश्न
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
If the points (a1, b1), (a2, b2) and(a1 + a2, b1 + b2) are collinear, then ____________.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.
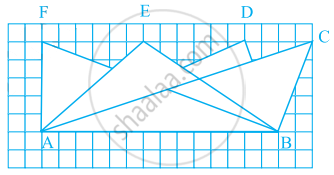
- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
Triangles having the same base have equal area.
In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

