Advertisements
Advertisements
Question
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
Solution
We know area of triangle formed by three points (x1y1) , (x2y2), and (x3y3)is given by `triangle=1/2 [x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
The vertices are given as `(at_1^2,2at1),(at_2^2,2at_2),(at_3^2,2at_3)`
`triangle =1/2[at_1^2(2at_2-2at_3)+at_2^2(2at_3-2at_1)+at_3^2(2at_1-2at_2)]`
`=1/2xx2a^2[(t_1^2t_2-t_1^2t_3)+(t_2^2t_3-t_2^2t_1)+(t_3^2t_1-t_3^2t_2)]`
`=a^2[(t_1^2t_2-t_2^2 t_1)+(t_2^2 t_3-t_1^2 t_3)+(t_3^2t_1-t_3^2 t_2)]`
`=a^2 [t_1t_2(t_1-t_2)+t_3 (t_2^2-t_1^2)+t_3^2 (t_1-t_2)]`
`=a^2[(t_1-t_2) {t_1t_2-t_3(t_2+t_1)+t_3^2)]`
`=a^2[(t_1-t_2){t_1t_2-t_3t_2-t_3t_1+t_3^2}`
`=a^2 [(t_1-t_2){t_2(t_1-t_3)-t_3 (-t_3+t_1)}]`
`=a^2[(t_1-t_2) (t_1-t_3)(t_2-t_3)]`
or,`triangle =a_2 (t_1-t_2) (t_2-t_3)(t_3-t_1)` assuming t1> t2, t2 > t3, t3 > t1
APPEARS IN
RELATED QUESTIONS
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
For what value of x are the points A(-3, 12), B(7, 6) and C(x, 9) collinear.
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
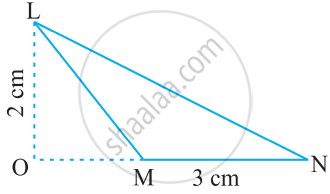
Find the area of the following triangle:
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 15 cm | 154.5 cm2 |
Area of a triangle = `1/2` base × ______.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
