Advertisements
Advertisements
प्रश्न
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
उत्तर
We know area of triangle formed by three points (x1y1) , (x2y2), and (x3y3)is given by `triangle=1/2 [x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
The vertices are given as `(at_1^2,2at1),(at_2^2,2at_2),(at_3^2,2at_3)`
`triangle =1/2[at_1^2(2at_2-2at_3)+at_2^2(2at_3-2at_1)+at_3^2(2at_1-2at_2)]`
`=1/2xx2a^2[(t_1^2t_2-t_1^2t_3)+(t_2^2t_3-t_2^2t_1)+(t_3^2t_1-t_3^2t_2)]`
`=a^2[(t_1^2t_2-t_2^2 t_1)+(t_2^2 t_3-t_1^2 t_3)+(t_3^2t_1-t_3^2 t_2)]`
`=a^2 [t_1t_2(t_1-t_2)+t_3 (t_2^2-t_1^2)+t_3^2 (t_1-t_2)]`
`=a^2[(t_1-t_2) {t_1t_2-t_3(t_2+t_1)+t_3^2)]`
`=a^2[(t_1-t_2){t_1t_2-t_3t_2-t_3t_1+t_3^2}`
`=a^2 [(t_1-t_2){t_2(t_1-t_3)-t_3 (-t_3+t_1)}]`
`=a^2[(t_1-t_2) (t_1-t_3)(t_2-t_3)]`
or,`triangle =a_2 (t_1-t_2) (t_2-t_3)(t_3-t_1)` assuming t1> t2, t2 > t3, t3 > t1
APPEARS IN
संबंधित प्रश्न
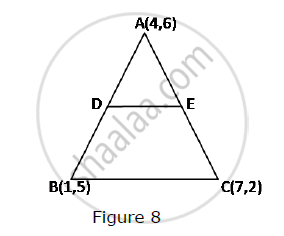
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
The points (1,1), (-2, 7) and (3, -3) are ______.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
