Advertisements
Advertisements
प्रश्न
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
उत्तर
We know area of triangle formed by three points (x1y1) , (x2y2), and (x3y3)is given by `triangle=1/2 [x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
The vertices are given as (a, c + a), (a, c) and (−a, c − a)
Δ = 1/2[a (c-c+a) + a(c-a-c-a)-a(c+a-c)
= 1/2[a(a)+a(2a)-a(a)]
= 1/2 [-2a2]=a2
APPEARS IN
संबंधित प्रश्न
Prove that the points (2, – 2), (–3, 8) and (–1, 4) are collinear
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
Find the area of the following triangle:
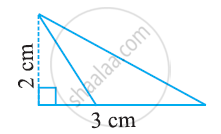
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
